페르게의 아폴로니오스
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
페르게의 아폴로니오스는 헬레니즘 시대에 활동한 고대 그리스의 수학자이자 천문학자로, 주로 기하학 분야에 기여했다. 그는 기원전 246년 이후 팜필리아의 페르가에서 태어났으며, 알렉산드리아에서 학문을 연구하고 저술 활동을 했다. 아폴로니오스는 '원뿔 곡선론'을 저술하여 원뿔 곡선에 대한 체계적인 연구를 수행했으며, 이심원과 주전원을 이용한 행성 운동 설명의 등가를 제시했다. 그의 저작은 후대에 큰 영향을 미쳤으나, '원뿔 곡선론'을 제외한 대부분의 작품은 소실되었다.
더 읽어볼만한 페이지
- 팜필리아인 - 미하일 아탈리아티스
미하일 아탈리아티스는 11세기 비잔틴 제국의 법률가, 관리, 역사가이자 작가로, 법학 연구와 관직 생활을 통해 《포네마 노미콘》 편찬, 《디아탁시스》 작성, 그리고 《역사》 기록 등 다양한 업적을 남겼다. - 그리스의 발명가 - 히파르코스
히파르코스는 기원전 2세기 중후반에 활동한 니카이아 출신의 고대 그리스 천문학자이자 수학자로, 삼각함수표 작성, 별의 밝기 등급 분류, 춘분점 세차 운동 발견, 정밀한 별 목록 편찬 등 천문학 발전에 크게 기여하여 "삼각법의 아버지"라 불린다. - 그리스의 발명가 - 에라토스테네스
에라토스테네스는 고대 그리스의 학자로서, 알렉산드리아 도서관의 관장을 역임하며 지구의 둘레를 정확하게 계산하고 에라토스테네스의 체를 고안하는 등 수학, 과학, 지리학 분야에서 다양한 업적을 남겼다. - 고대 그리스의 천문학자 - 사모스의 아리스타르코스
사모스의 아리스타르코스는 기원전 3세기 사모스 출신 천문학자로, 지구 중심설에 기반한 천체 계산법을 제시한 저서와 더불어 태양 중심설을 주장하여 코페르니쿠스 혁명의 선구자로 인정받고 있다. - 고대 그리스의 천문학자 - 히파르코스
히파르코스는 기원전 2세기 중후반에 활동한 니카이아 출신의 고대 그리스 천문학자이자 수학자로, 삼각함수표 작성, 별의 밝기 등급 분류, 춘분점 세차 운동 발견, 정밀한 별 목록 편찬 등 천문학 발전에 크게 기여하여 "삼각법의 아버지"라 불린다.
| 페르게의 아폴로니오스 - [인물]에 관한 문서 | |
|---|---|
| 기본 정보 | |
 | |
| 출생 | 기원전 240년경 |
| 사망 | 기원전 190년경 |
| 국적 | 고대 그리스 |
| 분야 | 기하학, 천문학 |
| 영향 | 원뿔 곡선론 아폴로니오스 문제 아폴로니오스 원 아폴로니오스 여과 |
2. 생애
아스칼론의 에우토키오스에 따르면, 기하학자 아폴로니오스는 프톨레마이오스 3세 에우에르게테스 시대에 팜필리아의 페르가 출신이었다.[2] 프톨레마이오스 3세 에우에르게테스는 디아도코이 계승의 이집트의 세 번째 그리스 왕조의 왕으로, 기원전 246–222/221년에 통치했다.[3] 페르가는 헬레니즘 시대의 도시로 아나톨리아의 팜필리아에 위치해 있었으며, 헬레니즘 문화의 중심지였다. 에우토키오스는 페르가를 프톨레마이오스 왕조와 연관시키는 것으로 보이지만, 당시 페르가는 셀레우코스 제국에 속해 있었다.[3] 기원전 3세기 후반 동안 페르가는 여러 차례 주인이 바뀌어 셀레우코스 왕조와 페르가몬 왕국의 아탈로스 왕조의 지배를 번갈아 받았다.[3] 아폴로니오스는 알렉산드리아에서 살고, 공부하고, 글을 쓴 것으로 알려져 있다.[3]
아폴로니오스는 기하학, 특히 원뿔 곡선 연구에 큰 업적을 남겼다. 그의 저서 《원뿔 곡선론》은 고대 그리스 수학의 정수로 꼽히며, 후대 수학 발전에 지대한 영향을 미쳤다.
그리스의 수학자이자 천문학자인 힙시클레스의 편지는 원래 유클리드의 ''원론'' 13권 중 일부인 유클리드의 14권 부록의 일부였다.[4] 이 편지에서 힙시클레스는 티레의 바실리데스가 알렉산드리아에서 아폴로니오스의 글을 연구하고, 그 내용이 정확하지 않다고 결론 내렸다고 언급한다.
'원뿔 곡선' 책의 서문에는 아폴로니오스가 영향력 있는 친구들에게 보낸 편지들이 담겨 있다. 처음 두 개의 서신은 페르가몬의 에우데모스에게 보내졌는데, 에우데모스는 페르가몬에 있는 박물관grc 연구 센터의 책임자였거나 나중에 그렇게 되었을 가능성이 높다. 아폴로니오스는 에우데모스에게 '원뿔 곡선'은 처음에는 알렉산드리아의 기하학자인 나우크라테스에 의해 요청받았다고 말하며, 나우크라테스에게 8권의 초고를 모두 제공했지만, "철저한 정화 없이"라고 언급하며, 책을 검증하고 수정하여 완성되는 대로 각각을 출판할 의도였다고 한다.
페르가몬을 방문한 아폴로니오스 본인에게 이 계획을 들은 에우데모스는 아폴로니오스에게 출판 전에 각 책을 자신에게 보내라고 주장했다. 알렉산드리아의 파푸스에 따르면 아폴로니오스는 유클리드의 학생들과 함께 알렉산드리아에 머물렀다고 한다.
첫 번째 서신과 두 번째 서신 사이에는 간격이 있다. 아폴로니오스는 아들인 아폴로니오스에게 두 번째 서신을 전달하도록 보냈으며, 에우데모스에게 특별 연구 그룹에서 이 책을 사용하라고 제안했다. 아폴로니오스는 에페소스에서 에우데모스에게 소개했고, 에우데모스의 제자가 된 기하학자 라오디케이아의 필로니데스를 만났다고 언급한다.
책 III의 서문은 사라졌고, 책 IV의 서문에서 아폴로니오스는 에우데모스가 사망했다고 말한다. 책 IV–VII의 서문은 더욱 형식적이며, 개인적인 정보를 생략한 단순한 요약이다. 이 네 권 모두 아탈로스에게 보내졌으며, 아폴로니오스는 "나의 작품을 소유하려는 당신의 간절한 열망 때문에" 선택했다고 말했다. 한 가지 이론은 아탈로스가 아탈로스 2세 필라델푸스(기원전 220–138년)이며, 페르가몬의 장군이자 수호자였다는 것이다.
서문 VII에서 아폴로니오스는 책 VIII을 "부록... 가능한 한 빨리 보내도록 주의하겠다"라고 묘사한다. 그것이 보내졌다는 기록은 없으며, 아폴로니오스가 그것을 끝내기 전에 사망했을 수도 있다. 그러나 알렉산드리아의 파푸스는 그것에 대한 보조정리를 제공했으므로, 어떤 형태로든 유통되었을 것이다.
3. 업적
아폴로니오스는 많은 저서를 집필했지만, 《원뿔 곡선》(Conics)만이 현존한다. 이 책은 총 8권으로 구성되어 있는데, 처음 4권만이 아폴로니우스의 그리스어 원본 텍스트로 남아있다. 5권에서 7권은 바누 무사가 의뢰하고 사비트 이븐 쿠라가 번역한 아랍어 번역본으로만 전해지며, 그리스어 원본은 소실되었다.[5] 8권은 초고 존재 여부만 알려져 있고, 최종 원고 작성 여부는 불확실하다.
《원뿔 곡선》은 유클리드식의 정의, 도형, 도형의 부분들을 제시하고, "주어진 것" 다음에 "증명해야 할" 명제가 이어진다. 1권에서 7권까지 총 387개의 명제가 제시되어 있다.
그리스 기하학자들은 아르키메데스처럼 공학 및 건축 응용에 필요한 그림 배치에 관심이 많았다. 당시에도 원뿔 곡선에 대한 수요가 컸으며, 수학적 특성 개발은 그리스 기하학적 대수 방향으로 이루어졌다. 이들은 측정 그리드와 데카르트 좌표계 사이의 중간 좌표계를 사용했고, 비례 이론과 면적 적용을 통해 시각적 방정식 개발이 가능했다.
"면적 적용"은 면적과 선분이 주어졌을 때, 이 면적이 선분의 제곱과 같은지 묻는 것이다. 아폴로니오스는 세로좌표의 제곱이 가로좌표에 대한 직사각형에 적용되는지 질문했다.[6]
프톨레마이오스는 저서 ''알마게스트''에서 아폴로니오스가 이심원과 주전원과 종원을 사용한 행성 운동 설명을 제시하고, 두 설명이 동등함을 보였다고 기록했다.
아폴로니오스의 저작 중 《원뿔 곡선》을 제외한 나머지는 단편적이거나 소실되었다. 소실된 작품들은 주로 해설자들의 언급을 통해 알려져 있으며, 문서 증거 없이 아폴로니오스의 것으로 추정되는 내용도 있지만 신뢰성은 불확실하다.
3. 1. 원뿔 곡선론
아폴로니우스는 많은 책을 쓴 기하학자였지만, 그의 저서 중 《원뿔 곡선론》만이 현존한다. 이 책은 총 8권으로 구성되어 있는데, 처음 4권만이 아폴로니우스가 직접 쓴 그리스어 원본으로 남아있다. 5권에서 7권은 바누 무사가 의뢰하고 사비트 이븐 쿠라가 번역한 아랍어 번역본으로만 전해지며, 그리스어 원본은 소실되었다.[5] 8권은 초고가 있었는지, 최종 원고가 작성되었는지는 알려지지 않았다. 에드먼드 핼리가 라틴어로 "재구성"한 것이 있지만, 이것이 아폴로니우스의 저작과 얼마나 유사한지는 알 수 없다.
《원뿔 곡선론》의 그리스어 원본은 유클리드의 방식을 따라 정의, 도형, 도형의 부분들을 제시하고, "주어진 것" 다음에 "증명해야 할" 명제를 제시한다. 1권에서 7권까지 총 387개의 명제가 제시되어 있다. 아폴로니우스는 각 권마다 계획을 세웠고, 이 계획은 《서문》에 부분적으로 설명되어 있지만, 주제의 논리적인 흐름에 더 의존했다.
1권에는 58개의 명제가 있으며, 원뿔과 원뿔 곡선에 관한 기본적인 정의들이 주된 내용이다. 원뿔 표면은 선분이 이등분선 점을 중심으로 회전하여 만들어지는데, 끝점은 각각 자체 평면에서 원을 그린다. 원뿔은 이중 원뿔 표면의 한쪽 가지로, 꼭짓점(또는 정점), 밑면인 원, 그리고 꼭짓점과 밑면의 중심을 연결하는 축으로 구성된다.
''단면''(라틴어 sectiola, 그리스어 tomegrc)은 평면으로 원뿔을 잘라낸 것이다.
그리스 기하학자들은 공학 및 건축의 다양한 응용 분야에서 선택한 그림을 배치하는 데 관심이 있었다. 원뿔 곡선에 대한 수요는 당시에도 있었고 지금도 있으며, 수학적 특성 개발은 그리스 기하학적 대수 방향으로 이끌었다. 그들은 측정 그리드와 데카르트 좌표계 사이의 중간 좌표계를 사용했다.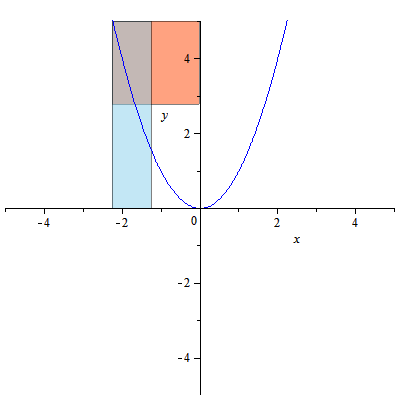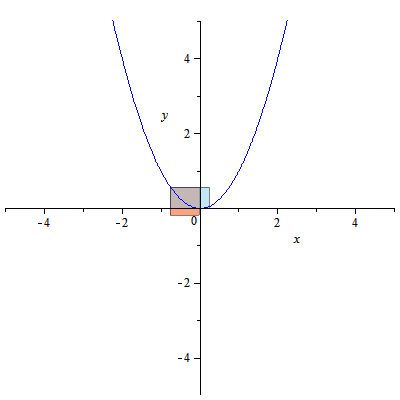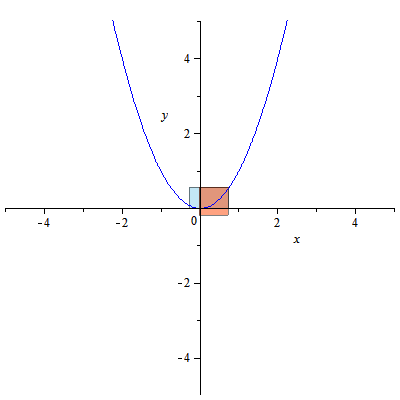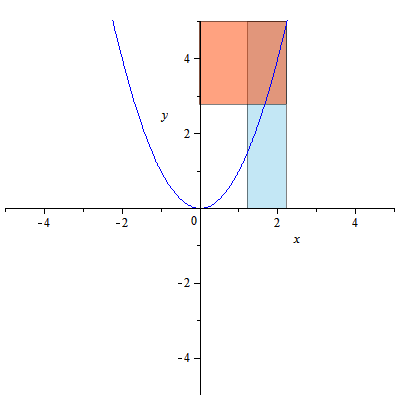
"면적 적용"은 주어진 면적과 선분이 있을 때 이 면적이 선분의 제곱과 같은지 묻는 것이다. 아폴로니오스는 세로좌표의 제곱이 가로좌표에 대한 직사각형에 적용되는지 질문했고,[6] 그렇다면 그의 방정식은 와 동일하며, 이는 포물선 방정식의 현대적 형태 중 하나이다. 그는 이 도형에 "적용"이라는 의미의 "포물선"이라는 이름을 붙였다.
"적용 불가능성" 사례는 또는 의 두 가지로 나뉜다. 전자의 경우, 는 ellipsisgrc("결핍")이라는 양만큼 에 미치지 못한다. 후자의 경우, 는 hyperbolegrc("과잉")이라는 양만큼 초과한다. 결핍을 보상하는 도형은 타원으로, 과잉을 보상하는 도형은 쌍곡선으로 명명되었다. 현대 방정식의 용어는 도형의 원점에서의 변환 및 회전에 따라 다르지만, 타원에 대한 일반 방정식은 로 표현될 수 있으며, 여기서 는 결핍이다. 쌍곡선에 대한 방정식은 가 되며, 여기서 는 과잉이다.
제2권에는 53개의 명제가 수록되어 있다. 아폴로니우스는 "지름과 축, 점근선 및 기타 사항과 관련된 속성"을 다루려고 했다.
제3권은 56개의 명제를 담고 있으며, "입체 자취의 구성에 사용되는 정리... 세 선 및 네 선 자취..."에 대한 정리에 대한 독창적인 발견을 주장한다. 세 선 자취 문제는 "세 개의 주어진 고정된 직선으로부터의 거리가 ... 한 거리의 제곱이 항상 다른 두 거리로 포함된 직사각형에 대한 일정한 비율을 갖는 점의 자취"를 찾는 것이며, 이것이 포물선을 생성하는 면적 적용에 대한 증명이다.[24] 네 선 문제는 타원과 쌍곡선을 생성한다.
제4권은 57개의 명제를 담고 있으며, "원뿔 단면이 서로 만날 수 있는 최대 점의 수, 또는 원의 원주와 만날 수 있는 최대 점의 수..."에 관한 것이다.
5권은 아랍어 번역을 통해서만 알려져 있으며, 77개의 명제를 담고 있다.[7] 타원은 50개, 포물선은 22개, 쌍곡선은 28개를 다루고 있다.[8] 최대 및 최소 선이라고 언급했지만, 명확한 설명은 없다.
6권은 아랍어 번역을 통해서만 알려져 있으며, 33개의 명제를 담고 있다. 주제는 "원뿔의 같고 유사한 부분"이다. 아폴로니우스는 합동과 유사성의 개념을 원뿔 곡선으로 확장한다.
제7권은 아랍어 번역본으로, 51개의 명제를 담고 있다. 지름과 "그 위에 묘사된 도형", 공액 지름에 대한 내용이다.
아폴로니오스는 저서 『원뿔 곡선론』(''Κωνικά'')에서 원뿔을 꼭짓점을 통과하지 않는 평면으로 절단한 단면의 도형인 "타원", "포물선", "쌍곡선"에 대해 상세한 연구를 진행했다. "타원", "포물선", "쌍곡선"의 명칭은 아폴로니오스가 각각 ellipsisgrc (부족하다), parabolegrc (일치하다), hyperbolegrc (초월하다)라고 부른 데에서 유래했다.[24]
3. 2. 천문학
아폴로니오스는 행성 운동에 대한 두 가지 설명, 즉 이심원과 주전원과 종원을 사용한 설명을 제시하였고, 이 두 설명이 동등하다는 것을 보였다. 프톨레마이오스는 그의 저서 ''알마게스트''에서 이러한 등가를 설명한다.[24] 또한, 아폴로니오스는 (현재 내용이 전해지는 것 중에서는 가장 오래된) 이심원과 종원과 주전원을 사용한 행성 이론을 전개하여 행성이 멈추는 현상을 설명하였다.
3. 3. 기타 저작
아폴로니오스의 저작 중 현재 전해지지 않는 작품들은 대부분 단편적이거나 소실되었다. 이 소실된 작품들은 주로 다른 학자들의 해설이나 언급을 통해 그 내용이 알려져 있다. 또한, 일부 학자들은 문서 증거 없이 아폴로니오스의 것이라고 주장하는 내용도 있으나, 그 신뢰성은 불확실하다.
파푸스는 『원뿔 곡선』 외에도 아폴로니오스의 다른 논문들을 언급했는데, 다음과 같다.
| 제목 | 번역 | 내용 |
|---|---|---|
| Λόγου ἀποτομή | 『비의 절단』 (De Rationis Sectione) | 두 개의 직선과 각 직선 위에 하나의 점이 주어졌을 때, 주어진 비를 갖는 선분을 그리도록 하는 문제 |
| Χωρίου ἀποτομή | 『넓이의 절단』 (De Spatii Sectione) | 두 절편으로 둘러싸인 직사각형이 주어진 직사각형과 같도록 하는 문제 |
| Διωρισμένη τομή | 『결정된 절단』 (De Sectione Determinata) | 선 위에 있는 점들이 다른 점들과 일정한 비율을 이루는 문제를 다룸 (1차원 해석 기하학) |
| Ἐπαφαί | 『접촉』 (De Tactionibus) | 주어진 점, 직선, 원에 접하는 원을 그리는 문제 (아폴로니우스 문제) |
| Νεύσεις | 『경사』 (De Inclinationibus) | 주어진 길이의 직선을 주어진 두 선 사이에 삽입하는 방법 |
| Τόποι ἐπίπεδοι | 『평면 자취』 (De Locis Planis) | 직선 또는 원인 자취와 관련된 명제 |
이들 각 저작은 두 권으로 나뉘어 있었으며, 파푸스에 따르면 유클리드의 『자료』, 『포리즈마』, 『표면 자취』, 그리고 아폴로니오스의 『원뿔 곡선』과 함께 고대 분석 기하학의 중요한 부분을 구성했다.[1]
17세기 후반, 핼리는 『비례 절단론』(De Rationis Sectione)과 『공간 절단론』(De Spatii Sectione)을 복원했다.[1] 『결정된 절단』(De Sectione Determinata)은 빌레브로트 스넬, 알렉산더 앤더슨, 로버트 심슨 등이 복원을 시도했다.[1] 『접촉』(De Tactionibus)은 비에트가 복원했고, 로마누스는 쌍곡선을 이용해 해결했다.[1] 『경사』(De Inclinationibus)는 마린 게탈디치, 휴고 도메리크, 새뮤얼 호슬리가 복원을 시도했다.[1] ''평면 기하학''은 피에르 드 페르마, 프란스 판 스호텐, R. 심슨이 복원을 시도했다.[1]
고대 작가들은 아폴로니오스의 다른 저작들도 언급했는데, 다음과 같다.
- Περὶ τοῦ πυρίου (페리 투 피리우): ''불태우는 거울에 관하여''라는 뜻으로, 포물선의 초점 특성을 다룬 논문으로 추정된다.
- Περὶ τοῦ κοχλίου (페리 투 코클리우): ''원통 나선에 관하여''라는 뜻으로, 프로클루스가 언급했다.
- 같은 구에 내접하는 십이면체와 이십면체의 비교
- Ἡ καθόλου πραγματεία (헤 카톨루 프라그마테이아): 수학의 일반 원리에 대한 저작으로, 유클리드 『원론』에 대한 비판과 제안을 포함했을 것으로 추정된다.
- Ὠκυτόκιον (오키토키온): "빠른 출산"이라는 뜻으로, π 값의 더 정확한 한계를 구하는 방법을 제시했다고 에우토키우스가 언급했다. 아르키메데스는 3을 상한, 3을 하한으로 계산했다.
- 산술 저작: 파푸스에 따르면, 큰 숫자를 표현하고 곱하는 시스템에 관한 내용이다.
- 무리수에 대한 이론: 유클리드, 제10권의 내용을 확장한 것으로, 뵈프케가 출판한 파푸스의 주석에서 발췌되었다.[1]
4. 영향
초기 인쇄본은 대부분 16세기에 나오기 시작했는데, 당시 유럽에서는 학술 서적을 신 라틴어로 쓰는 것이 일반적이었다. 라틴어로 쓰인 수학 원고가 거의 없었기 때문에 초기 인쇄본 편집자들은 그리스어나 아랍어에서 번역했다. 때로는 그리스어와 라틴어를 함께 제시하기도 했는데, 그리스어 텍스트는 원본이거나 편집자가 복원한 것이었다. 당시 비평적 논평은 주로 라틴어로 작성되었다. (이전 해설은 고대 또는 중세 그리스어나 아랍어로 작성되었다.) 18세기와 19세기가 되어서야 현대 언어로 된 판이 나오기 시작했다. 초기 인쇄본의 대표적인 목록은 다음과 같다.
| 저자 | 연도 | 제목 | 위치 | 출판사 | 언어 | 비고 |
|---|---|---|---|---|---|---|
| 아폴로니우스 | 1566 | Conicorum libri quattuor: una cum Pappi Alexandrini lemmatibus, et commentariis Eutocii Ascalonitae. Sereni Antinensis philosophi libri duo ... quae omnia nuper Federicus Commandinus Vrbinas mendis quampluris expurgata e Graeco conuertit, & commentariis illustrauit | Bononiae | Ex officina Alexandri Benatii | grc, la | 페데리쿠스 코만디누스가 그리스어로 쓴 원뿔 곡선 처음 4권과 그의 라틴어 번역본, 알렉산드리아의 파푸스, 아스칼론의 유토키우스, 안티노우폴리스의 세레누스의 해설이 실린 책. |
| 아폴로니우스, I. 배로우 | 1675 | Apollonii conica: methodo nova illustrata, & succinctè demonstrata | Londini | Excudebat Guil. Godbid, voeneunt apud Robertum Scott, in vico Little Britain | la | 아이작 배로우가 고대 그리스어에서 신 라틴어로 번역한 원뿔 곡선 처음 4권. 보스턴 공립 도서관에 있는 복사본은 존 애덤스 소유였다. |
| 아폴로니우스, 파푸스, E. 핼리 | 1706 | Apollonii Pergaei de sectione rationis libri duo: Ex Arabico ms. Latine versi. Accedunt ejusdem de sectione spatii libri duo restituti | Oxonii | la | 아폴로니우스의 분실되었지만 재구성된 두 작품 소개. De Sectione Rationis는 에드워드 버나드가 부분 번역했지만 그의 죽음으로 중단된 옥스퍼드 보들리안 도서관에 있는 아랍어 미출판 원고에서 가져온 것이다. 핼리 혜성 이름을 따서 명명된 교수이자 천문학자, 수학자, 탐험가인 에드먼드 핼리가 손상된 텍스트를 해독하지 못하고 포기했다. 데이비드 그레고리 (수학자)가 헨리 올드리치를 위해 아랍어를 복원했고, 올드리치는 다시 핼리에게 주었다. 아랍어를 배운 핼리는 De Sectione Rationis를 만들었고, 파푸스가 주석을 낸 De Sectione Spatii 버전을 신 라틴어로 번역했다. 두 신 라틴어 작품과 파푸스의 고대 그리스어 주석은 1706년 단일 책으로 묶였다. 아랍어 원고 저자는 알려지지 않았다. 825년 알마문 후원하에 작성되었다는 진술에 근거하여 핼리는 "Praefatio ad Lectorem"에서 이를 820년으로 추정한다. | |
| 아폴로니우스, 파푸스, 핼리, 유토키우스, 세레누스 | 1710 | Apollonii Pergaei Conicorum libri octo, et Sereni Antissensis De sectione cylindri & coni libri duo | Oxoniae | e Theatro Sheldoniano | la, grc | 1706년 출판된 데이비드 그레고리의 수정된 아랍어 텍스트 de Sectione rationis 번역 성공으로 핼리는 아폴로니우스 전체 원뿔 곡선을 복원하고 라틴어로 번역했다. 제1-4권은 그리스어와 핼리의 라틴어가 나란히 있는 형태로 나타난다. 제5-6권은 1626년 알레포에서 골동품 학자 야코부스 골리우스가 구입한 그리스어에서 아랍어로 이전에는 제대로 평가받지 못했던 번역본의 뜻밖의 발견에서 나왔다. 1696년 사망 후, 보들리안 도서관으로 넘어갔다(원래 MS Marsh 607, 1070년으로 연대 측정).[14] 훨씬 이전 제작된 번역본은 9세기 살았던 세 형제인 바누 무사 ("무사의 아들")로 불리는 알마문 학파에서 나왔다. 그들을 위해 일하는 작가들이 번역을 수행했다.[3] 핼리 작품에는 제5-7권 라틴어 번역만 실려 있다. 이것이 최초 인쇄 출판이다. 제8권은 알마문 학자들이 보존하기 전 분실되었다. 제7권에서 개발된 예상과 파푸스 보조 정리에 기초한 핼리의 조작은 라틴어로 제공된다. 유토키우스 주석, 파푸스 보조 정리, 세레누스 관련 두 논문이 원뿔 곡선 해석 지침으로 포함되었다. |
《원뿔 곡선》은 난해하여 후대 해설자들에게 지적 활동 여지를 제공했으며, 각 해설자는 자신 시대에 가장 명료하고 적절한 방식으로 아폴로니오스를 제시했다. 주석, 광범위한 서론, 다양한 형식, 추가 도면, 머리글 추가를 통한 피상적 재구성 등 다양한 방법을 사용했으며, 해석에는 미묘한 차이가 있다.
''원뿔 곡선론(Conics)''에 관해 영어로 쓰인 자료는 거의 없는데, 16~18세기 유럽 수학자, 특히 에드먼드 핼리, 아이작 뉴턴 같은 영국 수학자들은 신 라틴어를 선호했기 때문이다. 이후 몇 세기 동안 기하학은 좌표를 사용하여 재정립되었고 (해석 기하학), 종합적 방법은 선호도를 잃어, ''원뿔 곡선론(Conics)'' 직접적 영향력은 수학 연구에서 감소했다.
영어로 쓰인 발표 자료는 19세기 후반 시작되었다. 특히 영향력 큰 것은 토머스 히스가 번역한 《원뿔 곡선 논고(Treatise on Conic Sections)》이다. 그의 방대한 서문 해설에는 그리스어, 의미 및 용법을 제공하는 아폴로니오스 기하학 용어 사전이 포함되어 있다.[15] "이 논문 겉보기에는 방대한 양이 많은 사람들 접하는 것을 꺼리게 만들었다"고 논평하면서,[16] 그는 제목을 추가하고, 겉으로 조직을 변경하고, 현대적 표기법으로 텍스트를 명확히 할 것을 약속했다.
히스는 19세기 말과 20세기 초 활동했으며 1940년 사망했지만, 그동안 또 다른 관점이 발전했다. 세인트존스 칼리지 (애나폴리스/산타페)는 1936년 인증을 잃고 파산 직전 놓였다. 절망한 이사회는 시카고 대학교에서 고전 연구 위한 새로운 이론 프로그램 개발해 온 스트링펠로우 바, 스콧 뷰캐넌을 소환했다. 이 기회를 잡은 그들은 1937년 세인트존스에서 "새로운 프로그램" 시작했고, 나중에 위대한 고전 프로그램이라 불리게 되었다. 세인트존스에서는 아폴로니오스가 해석 기하학 부속물이 아닌, 그 자체로 가르쳐졌다.
아폴로니오스 "튜터"는 1937년 버지니아 대학교에서 박사 학위 받은 R. 케이트스비 탈리아페로였다. 그는 1942년까지, 그리고 1948년 1년 동안 튜터를 맡았으며, 프톨레마이오스 ''알마게스트''와 아폴로니오스 ''원뿔 곡선''을 직접 번역하여 영어 번역본을 제공했다. 이 번역본은 브리태니커 백과사전 서양 고전 시리즈 일부가 되었다. 책 I-III만 포함되었으며, 특별 주제에 대한 부록이 있다 (마이클 N. 프리드가 번역한 원뿔 곡선 책 IV는 2002년 출판되었다). 히스와 달리 탈리아페로는 아폴로니오스를 표면적으로라도 재구성하거나 다시 쓰려 시도하지 않았다. 현대 영어로 그의 번역은 그리스어를 매우 충실하게 따른다. 그는 어느 정도 현대적 기하학적 표기법을 사용한다.
탈리아페로 작업과 동시, 제2차 세계 대전 시대 옥스퍼드 대학교수였던 아이보어 토마스는 그리스 수학에 깊은 관심을 가지게 되었다. 그는 선집을 계획했고, 이는 그가 로열 노퍽 연대 장교로 군 복무 하는 동안 결실을 맺었다. 전쟁 후, 이 선집은 로브 고전총서에 수록되어 토마스가 번역한 2권으로 출판되었으며, 로브 시리즈 관례대로 페이지 한쪽에는 그리스어 원문, 다른 쪽에는 영어 번역본이 실렸다. 토마스 작업은 그리스 수학 황금기 연구하는 데 있어 지침서 역할을 했다. 아폴로니오스 경우, 그는 주로 제1권에서 원뿔 곡선을 정의하는 부분만 포함시켰다.
히스에 따르면,[18] "아폴로니오스 방법"은 그에게 개인적인 것이 아니었으며, 그가 후대 이론가들에게 미친 영향은 그의 기술 혁신이 아닌 기하학 영향이었다. 히스는 다음과 같이 말한다.
> 원뿔 곡선에서 사용된 방법들을 자세히 고려하기 전, 일반적으로 이 방법들은 유클리드 《원론》에서 최종적으로 표현된 기하학적 탐구 보편적 원칙을 꾸준히 따른다고 말할 수 있다.
고대 황금기 기하학자들을 언급할 때, 현대 학자들은 "방법"이라는 용어를 오늘날 대수학에서 생성된 결과와 동등한 결과를 기하학자가 시각적으로 재구성하는 방식으로 이해한다. 간단한 예로, 정사각형 넓이를 계산하는 대수적 방법은 변 길이를 제곱하는 것이며, 이와 유사한 기하학적 방법은 시각적 정사각형을 구성하는 것이다. 황금 시대 기하학적 방법은 초등 대수학 대부분 결과를 생성할 수 있었다.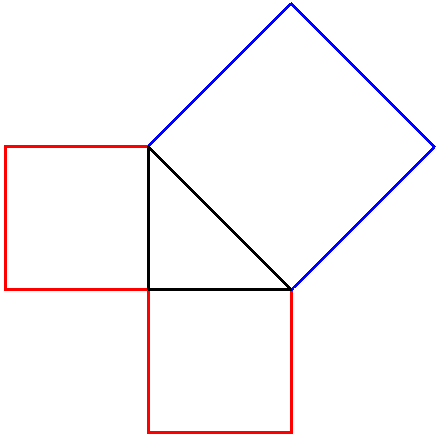
히스는 황금 시대 전체 방법에 대해 "기하학적 대수"라는 용어를 사용한다. 이 용어는 1890년 또는 그 이전 Henry Burchard Fine에 의해 정의되었으며, 분석 기하학 첫 번째 본격적 작품인 르네 데카르트 라 지오메트리에 적용되었다.[19] “근본적 연산이 형식적으로 동일한 두 대수는 형식적으로 동일하다”는 전제 조건을 설정하면서, Fine은 데카르트 작업이 “단순한 수치적 대수가 아니라, 더 나은 이름이 없어 선분 대수라고 부를 수 있는 것이다. 그 기호는 수치적 대수와 동일하다; ....”라고 말한다.
예를 들어 아폴로니오스에서 선분 AB(점 A와 점 B 사이 선)는 세그먼트 수치적 길이이기도 하다. 어떤 길이든 가질 수 있다. 따라서 AB는 3과 같은 임의 값이 할당될 수 있는 ''x''(미지수)와 같은 대수적 변수와 동일해진다.
변수는 아폴로니오스에서 "AB를 단면 임의의 점에서 지름까지 거리로 하자"와 같은 단어 구문으로 정의되며, 이는 오늘날 대수학에서도 계속되는 관행이다. 아폴로니오스에게는 그러한 규칙이 없었다. 그의 해법은 기하학적이었다.
그림으로 표현하기 어려운 관계는 그의 이해 범위를 벗어났지만, 그의 그림 해법 레퍼토리는 오늘날 일반적으로 알려지지 않은 복잡한 기하학적 해법 풀에서 나왔다. 잘 알려진 예외 중 하나는 필수적 피타고라스 정리이며, 현재에도 a2 + b2 = c2와 같은 표현을 설명하는 변에 정사각형이 있는 직각 삼각형으로 표현된다. 그리스 기하학자들은 이러한 항들을 "AB 위 정사각형" 등으로 불렀다. 마찬가지로 AB와 CD로 형성된 직사각형 면적은 "AB와 CD 위 직사각형"이었다.
이러한 개념은 그리스 기하학자들에게 선형 방정식과 이차 함수에 대한 대수적 접근성을 제공했으며, 후자는 원뿔 곡선이다. 이들은 각각 1 또는 2 지수를 포함한다. 아폴로니오스는 원뿔이 고체임에도 불구, 세제곱(입체 기하학에서 특징)에 대해 별로 사용하지 않았다. 그의 관심은 평면 도형인 원뿔 곡선에 있었다. 4 이상 거듭제곱은 기하학에서는 사용할 수 없지만 대수학에서는 쉽게 사용할 수 있는 추상화 정도가 필요하여 시각화를 넘어섰다.
일반적 공적 단위, 예를 들어 인치를, 자와 같은 표준 공적 도구를 사용하여 길이를 측정하는 모든 방법은 데카르트 격자를 암묵적으로 의미한다. 고대 그리스 측정 단위는 청동기 시대부터 그리스 수학자들에게 그러한 격자를 제공했다.
아폴로니우스 이전에는 메나이크무스, 아르키메데스가 이미 낮게 측정되는 좌측 수직선과 낮게 측정되는 하단 수평선을 기준으로 하는 거리를 참조하여 일반적 격자 암묵적 윈도우에 도형을 배치하기 시작했다. 방향은 직선 또는 서로 수직이다.[20] 이 윈도우 가장자리는 데카르트 좌표계에서 축이 된다. 임의의 점으로부터 축까지 직선 거리를 좌표로 지정한다. 고대 그리스인들은 그런 관례를 가지고 있지 않았다. 그들은 단순히 거리를 언급했다.
아폴로니우스는 그의 도형을 배치하는 표준 윈도우를 가지고 있다. 수직 측정은 그가 "지름"이라 부르는 수평선에서 시작된다. 이 단어는 그리스어와 영어에서 동일하지만 그리스어 이해 범위가 약간 더 넓다.[21] 원뿔 곡선 도형이 평행선 격자에 의해 잘리면, 지름은 도형 분기점 사이에 포함된 모든 선분을 이등분한다. 그것은 정점(koruphe, "왕관")을 통과해야 한다. 따라서 지름은 포물선 같은 열린 도형뿐 아니라 원 같은 닫힌 도형도 포함한다. 지름이 평행선에 수직이어야 한다는 규정은 없지만 아폴로니우스는 직선만 사용한다.
곡선 위 한 점에서 지름까지 직선 거리는 그리스어로 tetagmenos라 불리며, 어원적으로 단순히 "확장된"이라는 의미이다. 그것은 "아래로"(kata-) 또는 "위로"(ana-)만 확장되므로 번역가들은 그것을 종좌표로 해석한다. 이 경우 지름은 x축이 되고 정점은 원점이 된다. y축은 정점에서 곡선에 접선이 된다. 가로좌표는 종좌표와 정점 사이 지름 선분으로 정의된다.
아폴로니우스는 자신 좌표계 버전을 사용하여 원뿔 곡선에 대한 방정식 기하학적 등가물을 그림 형태로 개발하며, 그의 좌표계를 데카르트 좌표계로 간주할 수 있는지에 대한 질문을 제기한다. 몇 가지 차이점이 있다. 데카르트 좌표계는 모든 계산 수행하기 전 모든 공간 모든 도형을 포괄하는 보편적인 것으로 간주된다. 두 개의 교차하는 축으로 나뉜 네 개 사분면을 가지고 있다. 사분면 중 세 개는 0 기준 축과 반대 방향을 의미하는 음 좌표를 포함한다.
아폴로니우스는 음수를 가지지 않고, 명시적으로 0에 대한 숫자를 가지지 않으며, 원뿔 곡선과 독립적으로 좌표계를 개발하지 않는다. 그는 본질적으로 제1사분면에서만 작동하며, 모든 좌표가 양수이다. 따라서 현대 수학 역사가인 칼 보이어는 다음과 같이 말한다.
> 그러나 그리스 기하학적 대수는 음 크기를 제공하지 않았다. 더욱이, 좌표계는 모든 경우에 주어진 곡선 위에 사후적으로 중첩되어 그 속성을 연구했다.... 고대 최고 기하학자인 아폴로니우스는 해석 기하학을 개발하지 못했다....
그럼에도 불구, 보이어에 따르면 아폴로니우스 곡선 처리는 어떤 면에서는 현대적 처리와 유사하며, 그의 작업은 해석 기하학을 예견하는 것처럼 보인다. 아폴로니우스를 읽을 때는 그의 용어에 현대적 의미를 부여하지 않도록 주의해야 한다.
아폴로니오스는 유클리드 ''원론'' 5권과 6권에 표현된 "비례 이론"을 사용했다. 크니도스의 에우독소스가 고안한 이 이론은 순수하게 그래픽적 방법과 현대적 수론 사이 중간 단계에 있다. 표준 십진법과 분수에 대한 표준적 취급법이 부족하다. 그러나 명제는 산술에서 분수를 조작하는 규칙을 단어 형태로 표현한다. 히스는 그것들이 곱셈과 나눗셈을 대신한다고 제안한다.[22]
에우독소스는 "크기"라는 용어를 통해 숫자를 넘어 크기에 대한 일반적 의미, 즉 여전히 유지되는 의미를 부여하고자 했다. 유클리드 도형과 관련하여, 이는 가장 흔하게는 숫자, 즉 피타고라스 학파 접근 방식을 의미했다. 피타고라스는 우주가 양으로 특징지어질 수 있다고 믿었고, 이 믿음은 현재 과학적 정설이 되었다. 유클리드 5권은 크기(megethos, "크기")가 단위(meros, "부분")로 균등하게 나눌 수 있어야 한다고 주장하며 시작한다. 따라서 크기는 단위 배수이다. 이는 미터나 피트 같은 표준 측정 단위일 필요는 없다. 하나의 단위는 임의 지정된 선분일 수 있다.
다음은 과학에서 지금까지 고안된 가장 유용한 기본 정의일 것이다. 비율(그리스어 로고스, 대략 "설명" 의미)은 상대적 크기에 대한 진술이다. 두 크기, 예를 들어 선분 AB와 CD가 주어졌을 때, CD를 단위로 간주할 때 AB와 CD 비율은 AB에 있는 CD 수이다. 예를 들어, 4개 중 3개 부분, 또는 백만 분의 60개 부분, 여기서 ppm은 여전히 "부분" 용어를 사용한다. 비율은 현대적 분수 기초가 되며, 이는 또한 "부분" 또는 "조각" 의미하며, 파편이라는 단어와 동일한 라틴어 뿌리에서 유래한다.
비율은 "비례"라고 하는 논리적 구조에서 수학적 예측 기초가 된다(그리스어 아날로고스). 비례는 두 선분 AB와 CD가 다른 두 선분 EF와 GH와 동일한 비율을 갖는다면, AB와 CD는 EF와 GH에 비례하거나, 유클리드 표현에 따르면 AB 대 CD는 EF 대 GH와 같다고 말한다.
대수는 이 일반적 개념을 AB/CD = EF/GH 식으로 축소한다. 임의 세 항이 주어지면, 네 번째 항을 미지수로 계산할 수 있다. 위 식을 재정렬하면 AB = (CD/GH)•EF를 얻으며, y = kx로 표현될 때 CD/GH는 "비례 상수"로 알려져 있다. 그리스인들은 (그리스어 pollaplasiein)를 반복적으로 더하는 방식으로 쉽게 수행했다.
아폴로니오스는 거의 전적으로 선분과 면적 비율을 사용하며, 이는 정사각형과 직사각형으로 지정된다. 번역가들은 1684년 라이프니츠가 ''Acta Eruditorum''에서 도입한 콜론 표기법을 사용하기로 했다.[23] 다음은 ''원뿔 곡선'', 1권, 명제 11 예이다.
:그리스어 직역: BC (제곱)이 BAC (직사각형)에 FH가 FA에 있는 것과 같게 만들자
:탈리아페로 번역: "BC sq.: rect. BA.AC :: FH : FA"
:대수적 등가: BC2/BA•BC = FH/FA
5. 평가
《원뿔 곡선》의 난해함은 후대의 수학자들이 각자의 시대에 맞게 아폴로니오스의 이론을 명확하게 설명하고 확장하려는 시도를 불러일으켰다. 주석, 서론, 다양한 형식, 추가 도면, 부가 설명 등의 방법을 통해 아폴로니오스의 업적을 재해석하려는 노력이 이루어졌다.[15]
16~18세기 유럽, 특히 영국의 수학자들은 신 라틴어를 선호했기에 영어로 된 자료는 거의 없었다. 이후 해석 기하학의 발전으로 종합적인 방법은 인기를 잃었고, 《원뿔 곡선론》에 대한 직접적인 연구는 줄어들었다.
19세기 후반, 영어로 된 자료가 등장하기 시작했다. 특히 토머스 히스(Thomas Heath)의 《원뿔 곡선 논고(Treatise on Conic Sections)》 번역본은 방대한 해설과 함께 아폴로니오스의 기하학 용어 사전을 제공하여 큰 영향을 미쳤다.[15] 히스는 텍스트를 현대적 표기법으로 명확히 하고, 제목을 추가하여 가독성을 높였다.[16]
1937년, 스트링펠로우 바와 스콧 뷰캐넌은 세인트존스 칼리지에서 위대한 고전 프로그램을 시작하며 아폴로니오스를 해석 기하학의 부속물이 아닌 독립적인 학문으로 가르쳤다.
R. 케이트스비 탈리아페로는 아폴로니오스의 《원뿔 곡선》을 영어로 번역하여 브리태니커 백과사전의 서양 고전 시리즈에 포함시켰다. 그는 그리스어 원문에 충실하게 번역하면서 현대적인 기하학적 표기법을 일부 사용했다.
아이보어 토마스는 로브 고전총서를 통해 그리스 수학 선집을 출판했다. 그는 아폴로니오스의 원뿔 곡선 정의 부분을 그리스어 원문과 영어 번역본을 함께 수록하여 제공했다.
히스에 따르면,[18] 아폴로니오스의 방법은 개인적인 것이 아니라 원론에 표현된 기하학적 탐구의 보편적인 원칙을 따랐다.
히스는 황금 시대의 기하학적 방법을 "기하학적 대수"라고 칭했다.[19] 이는 르네 데카르트의 라 지오메트리에 적용된 개념으로, 선분을 수치적 길이로 취급하여 대수적 연산과 유사하게 다루는 방식이다.
아폴로니오스는 선분 AB를 대수적 변수처럼 취급하고, 단어 구문으로 변수를 정의했다. 그는 기하학적 해법을 사용했지만, 그림으로 표현하기 어려운 관계는 다루지 않았다.
아폴로니오스는 도형을 배치하는 표준 윈도우를 사용했다. 그는 "지름"이라고 부르는 수평선을 기준으로 수직 거리를 측정했다. 곡선 위의 한 점에서 지름까지의 직선 거리는 종좌표로 해석되며, 지름은 x축, 정점은 원점이 된다. y축은 정점에서 곡선에 접선이 된다. 가로좌표는 종좌표와 정점 사이의 지름의 선분으로 정의된다.
아폴로니오스는 원뿔 곡선에 대한 방정식의 기하학적 등가물을 그림 형태로 개발했다. 그러나 그는 음수를 사용하지 않았고, 명시적인 0의 개념도 없었으며, 좌표계를 원뿔 곡선과 독립적으로 개발하지 않았다. 그는 제1사분면에서만 작업했다. 현대 수학 역사학자인 칼 보이어는 아폴로니오스가 해석 기하학을 개발하지 못했다고 평가했다.
아폴로니오스는 유클리드의 ''원론'' 5권과 6권에 표현된 크니도스의 에우독소스의 "비례의 이론"을 사용했다. 이는 순수 그래픽적인 방법과 현대 수론 사이의 중간 단계에 해당한다. 비례는 두 크기의 상대적인 크기에 대한 진술이며, 현대 분수의 기초가 된다. 아폴로니오스는 선분과 면적의 비율을 주로 사용했으며, 번역가들은 콜론 표기법을 사용했다.[23]
참조
[1]
웹사이트
Apollonius and Conic Sections
https://math.uh.edu/[...]
2021-02-12
[2]
서적
Commentary on Conica
[3]
간행물
[4]
웹사이트
The thirteen books of Euclid's Elements
https://archive.org/[...]
Cambridge University Press
[5]
간행물
[6]
간행물
[7]
간행물
[8]
간행물
[9]
간행물
[10]
간행물
[11]
간행물
[12]
간행물
[13]
간행물
[14]
웹사이트
Arabic Manuscripts in the Bodleian Library
http://www.islamicma[...]
[15]
간행물
[16]
간행물
[17]
논문
A Tisket, a Tasket, an Apollonian Gasket
http://www.americans[...]
2015-02-05
[18]
간행물
[19]
서적
The number-system of algebra treated theoretically and historically
Leach
[20]
간행물
[21]
간행물
[22]
간행물
[23]
서적
A history of mathematical notations
https://archive.org/[...]
Dover Publications
[24]
문서
일본대백과전서(니포니카)
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com